rangkuman materi GELOMBANG MEKANIK dan contoh soal
rangkuman materi, rumus dan contoh soal
GELOMBANG MEKANIK
gelombang mekanik adalah gelombang yang membutuhkan medium dalam perambatannya
A. Gelombang berjalan
adalah gelombang yang nilai amplitudonya tetap
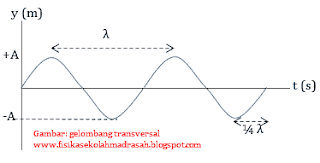
Persamaan umum gelombang berjalan
y = ± A sin (ωt ± kx )
Persamaan umum gelombang berjalan jika diketahui sudut fase awal (θo)
y = ± A sin (ωt ± kx + θo)
rumus cepat rambat gelombang
v = λ . f
keterangan:
y = simpangan (m)
A = amplitude (m)
+ A jika gelombang start ke atas
- A jika gelombang start ke bawah
ω = kecepatan sudut (rad/s)
rumus ω :
ω = 2 π f
f = frekuensi (Hz)
θo = sudut fase awal (rad)
k = tetapan gelombang (m-1)
+ k jika gelombang bergerak ke kanan
- k jika gelombang bergerak ke kanan
Rumus k:
2 π
k = -------
λ
θo = sudut fase awal (rad)
rumus beda fase gelombang
Δφ = f . Δt
atau:
B. gelombang stasioner
adalah gelombang yang nilai amplitudonya berubah

1. GS. Ujung terikat / tetap
untuk gelombang stasioner ujung terikat saat berada di ujung pantul (x = 0) terbentuk simpul (y=0)
Amplitudo Stasioner (As) gelombang stasioner ujung terikat
untuk gelombang stasioner ujung bebas saat berada di ujung pantul (x = 0) terbentuk simpul (y =maximum)
agar lebih faham dan untuk contoh soal berikut adalah link 50 soal gelombang mekanik beserta pembahasnnya bebrbentuk soal pilihan ganda dan uraian / esai
atau buka menu kemudian klik pembahasan soal fisika
GELOMBANG MEKANIK
gelombang mekanik adalah gelombang yang membutuhkan medium dalam perambatannya
A. Gelombang berjalan
adalah gelombang yang nilai amplitudonya tetap

Persamaan umum gelombang berjalan
y = ± A sin (ωt ± kx )
Persamaan umum gelombang berjalan jika diketahui sudut fase awal (θo)
y = ± A sin (ωt ± kx + θo)
rumus cepat rambat gelombang
v = λ . f
keterangan:
y = simpangan (m)
A = amplitude (m)
+ A jika gelombang start ke atas
- A jika gelombang start ke bawah
ω = kecepatan sudut (rad/s)
rumus ω :
ω = 2 π f
f = frekuensi (Hz)
θo = sudut fase awal (rad)
k = tetapan gelombang (m-1)
+ k jika gelombang bergerak ke kanan
- k jika gelombang bergerak ke kanan
Rumus k:
2 π
k = -------
λ
θo = sudut fase awal (rad)
rumus sudut fase gelombang:
θ = ωt
atau
θ = kx
rumus beda sudut fase gelombang:
Δθ = ω . Δt
atau
Δθ = k . Δx
rumus fase gelombang:
ωt
φ = --------- = f.t
2 π
atau:
kx x
φ = --------- = -----
2 π λ
Δφ = f . Δt
atau:
Δx
φ = -----
λ
adalah gelombang yang nilai amplitudonya berubah

1. GS. Ujung terikat / tetap
untuk gelombang stasioner ujung terikat saat berada di ujung pantul (x = 0) terbentuk simpul (y=0)
persamaan gelombang stasioner ujung terikat / tetap
y = 2A sin kx cos ωtAmplitudo Stasioner (As) gelombang stasioner ujung terikat
As = 2A sin kx
letak simpul dari ujung pantul (Xn) gelombang stasioner ujung terikat :
letak simpul dari ujung pantul (Xn) gelombang stasioner ujung terikat :
Xn = (n – 1) . ½ λ
Letak perut ujung pantul (Xn):
Xn = (2n – 1) . ¼ λ
2. GS. Ujung terbuka / bebas
untuk gelombang stasioner ujung bebas saat berada di ujung pantul (x = 0) terbentuk simpul (y =maximum)
persamaan gelombang stasioner ujung terbuka / bebas
y = 2A cos kx sin ωtamplitude stasioner
As = 2A cos kx
letak perut
Xn = (n – 1) . ½ λ
Letak simpul gelombang stasioner ujung bebas
Xn = (2n – 1) . ¼ λ
agar lebih faham dan untuk contoh soal berikut adalah link 50 soal gelombang mekanik beserta pembahasnnya bebrbentuk soal pilihan ganda dan uraian / esai
- PEMBAHASAN SOAL GELOMBANG MEKANIK (part 1/3)
- PEMBAHASAN SOAL GELOMBANG MEKANIK (part 2/3)
- PEMBAHASAN SOAL GELOMBANG MEKANIK (part 3/3)
atau buka menu kemudian klik pembahasan soal fisika


Comments
Post a Comment