Pelajaran Fisika

Soal dan Penyelesaian Fisika SMA -Alkisah, seorang anak (ngakunya siswa Rumah Belajar O-Brain) bertanya pada Newton dan Einstein tentang sesuatu hal. Ternyata ahli-ahli Fisika yang lain juga turut "nimbrung" menjawab sesuai hukum fisika yang mereka buat. Seru jadinya... Pertanyaannya: "Kenapa ya kalau bebek-bebek menyeberang jalan selalu berbaris bersama dan mengikuti pemimpinnya dengan baik?"

Soal dan Penyelesaian Fisika - Transformator atau trafo dan Prinsip Kerjanya, Transformator (Trafo) adalah alat yang dapat mengubah besar tegangan AC ke taraf tegangan lainnya menjadi lebih besar atau lebih kecil  dalam frekuensi yang sama. Fungsi ini juga dikenal dengan istilah step up dan step down. Lebih komplit tentang transformator, silahkan pelajari artikel sebelumnya berjudul: GGL

Cara menentukan besar resistor total atau pengganti, kuat arus dan beda tegangan tiap ujung resistor dan cabang rangkaian resistor campuran seri dan parelel resistor tiga cabang: Tentukan besar hambatan pada resistor paralel kemudian di seri Hitung arus total dengan rumus hukum ohm [ V = I . R ] tentukan besar kuat arus pada resistor yang di rangkai seri [ Iseri = Itotal ] hitung kuat arus pada tiap cabang resistor paralel dengan perbandingan terbalik Hitung beda potensial atau tegangan pada tiap tiap resistor dengan rumus hukum ohm [ V = I . R ] Perhatikan contoh berikut: Step 1: menghitung R paralel dan seri 1/Rp = 1/2 + 1/3 + 1/6 1/Rp = 3/6 + 2/6 + 1/6 1/Rp = 6/6 Rp = 1 Rs = 1 + 4 = 5 Step 2: menghitung I total V = I . R 20 = I . 5 I = 4 A Step 3: menghitung I pada resistor yg dirangkai seri I4 = Itot I4 = 4 A Step 4: menghitung arus tiap cabang resistor paralel dengan perbandingan terbalik R2 : R3 : R6 1/2 : 1/3 : 1/6 3/6 : 2/6 : 1/6 Sehingga perbandingan R2 : R3 : R6 = 3 : 2 : 1 A

Soal dan Penyelesaian Fisika - Rumus, Definisi dan penjelasan - Beberapa rumus Fisika yang paling penting dan paling sering digunakan, kami disajikan dan dijelaskan di bawah ini. Kami berharap dapat membantu teman-teman pembaca. A. Kecepatan Relatif Rumus, Definisi dan penjelasan \begin{align*}v_{AC}&=v_{AB}+v_{BC}\end{align*} $v_{AC}$ kecepatan A relatif terhadap C (vektor) $v_{AB}$

Daftar Isi Konsep rapat massa Sistem koordinat silinder dan sistem koordinat bola Sistem koordinat silinder Sistem koordinat bola Teorema sumbu sejajar Teorema sumbu tegak lurus Penurunan rumus momen inersia berbagai benda Batang silinder pejal Pelat tipis Silinder Bola Ekstra TIme Segitiga Kerucut Gambar 1. Momen inersia berbagai benda Saat mempelajari materi dinamika rotasi , tentu kalian pernah melihat gambar di atas ,Tapi pernahkah kalian berpikir asal dari persamaan-persamaan di atas? Berdasarkan hasil literasi dari berbagai sumber yang ada , Pada kesempatan kali ini saya akan mencoba melakukan penurunan rumus momen inersia untuk berbagai benda di atas sehingga ditemukan rumus-rumus dan angka di atas. Penurunan rumus momen inersia untuk berbagai benda di atas, pada dasarnya menggunakan persamaan umum momen inersia yang sudah pernah saya bahas di metari dinamika rotasi untuk kelas 11 yakni Persamaan di atas, merupakan persamaan dasar untuk semua jenis benda dengan massa yang terdis

cara menentukan arus pada rangkaian resistor campuran 1 seri dan 2 paralel yang dihubungkan dengan arus searah / DC: hitung hambatan total, paralel terlebih dahulu kemudian seri hitung arus total dengan rumus hukum ohm Tentukan arus pada rangkaian seri yaitu sama dengan arus total Tentukan arus pada rangkaian paralel dengan perbandingan terbalik Tentukan nilai tegangan tiap resistor dengan rumus V = I . R Konsep hukum kirchoff I pada rangkaian seri paralel 1. Rangkaian seri Rs = R1 + R2 + R3 + ..... Itot = Iseri = I1 + I2 + I3 + .... Vs = I . R atau Vs = V1 + V2 + V3 + ... 2. Rangkaian paralel  I/Rp = 1/R1 + 1/R2 + 1/R3 + .... Vp = V1 = V2 = V3 = .... Ip = Vp / Rp atau Ip = I1 + I2 + .... perhatikan contoh soal berikut : contoh soal no. 1 tentukan besar arus dan beda tegangan / potensial pada tiap resistor! Pembahasan : - step 1: menghitung hambatan total  Rangkaian paralel : 1/Rp = 1/15 + 1/30 1/Rp = 2/30 + !/30 1/Ro = 3/30 Rp = 30/3 = 10 Ω Rangkaian seri: Rs = 20 + 10 = 30 Ω - step 2

Soal Dan Penyelesaian Fisika SMA - Dimensi adalah cara penulisan suatu besaran dengan menggunakan simbol (lambang) besaran pokok, yang menunjukkan cara besaran itu tersusun dari besaran-besaran pokok. Dimensi suatu besaran yang dinyatakan dengan lambang huruf tertentu, biasanya diberi tanda [ ] A. Dimensi BESARAN POKOK Tabel lambang Dimensi besaran-besaran pokok. Besaran Pokok

Rumus energi kinetik rotasi Ek = 1/2 . I . ω² Rumus energi kinetik translasi Ek = 1/2 . m . v² Rumus saat benda menggelinding (bergerak translasi dan rotasi sekaligus) Ek = 1/2 . m . v² +  1/2 . I . ω² Atau: Ek = 1/2 . m .v² (1 + k) dimana k = konstanta momen inersia benda tegar Energi mekanik EM = m.g.h + 1/2 . m . v² +  1/2 . I . ω² Hukum kekekalan energi mekanik EM1 = EM2 Contoh soal 1. Soal fisika UN 2018 no.9 Sebuah silinder pejal (I = ½ MR 2  ) bermassa 8 kg menggelinding tanpa Slip padasuatu bidang  datar dengan kecepatan 15 m/s . Energi kinetik total silinder adalah  A 1.800 J B. 1.350 J C. 900 J D. 450 J E. 225 J Pembahasan: Ek = ½ m. v 2  ( 1 + k) = ½ . 8 . 15 2  (1 + ½) = 4. 225 . 3/2 = 1350 joule (keterangan: k adalah koefisien momen inersia benda tegar atau I ) 2. sebuah silinder tipis berongga ( I = M.R 2  ) dengan massa 2 kg dan jari - jari 10 cm mrnggelinding dari puncak bidang miring seperti gambar berikut. berapakah kecepatan silinder tersebut saat di tanah? penyelesa

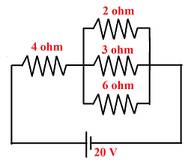
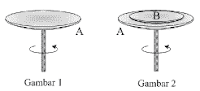
Rumus momentum sudut: L = I . ω Hukum kekekalan momentum pada gerak melingkar L = L' I . ω = I' . ω' Contoh soal: 1. Soal un fisika 2019 Pada saat piringan A berotasi 120 rpm (Gambar l), piringan B diletakkan di atas piringan A (Gambar 2) sehingga kedua piringan berputar dengan poros yang sama Massa piringan A = 100 gram dan massa piringan B = 300 gram, sedangkan jari-jari piringan A = 50 cm dan jari-jari piringan B = 30 cm, Jika momen inersia piringan adalah 1/2 m.R², maka besar kecepatan sudut kedua piringan pada waktu berputar bcrsama sama adalah .... A. 0,67 π rad. s -l B. 0,83 π rad. s -l C. 1,92 π rad. s -l D. 4,28 π rad. s -l E. 5,71 π rad. s -l Kunci jawaban: C Pembahasan: Rumus Hukum kekekalan momentum sudut: I1.ω1 + I2.ω2 = I1.ω1' + I2.ω2' 1/2.m1.R1².ω+0 = (1/2.m1.R1²+1/2.m2.R2² )ω' 1/2.100.50².120 = (1/2.100.50²+1/2.300.30²).ω' 15000000 = (125000 + 135000).ω' ω' = 1500/26 = 57,7 rpm ω' = 57,7 . [2π/60] = 1,92 π rad/s 2. Usbn 2017 Perha

Gambar 1. Atlet judo ketika membanting lawannya Seorang atlet judo ketika akan membanting lawannya, ia akan berusaha menempatkan titik pusat massa lawannya sedekat mungkin dengan pusat massa dirinya untuk mengurangi torsi yang disebabkan oleh lawannya tersebut, sehingga hanya torsi dirinya sendiri yang bekerja pada saat membanting. Berbicara tentang gerak rotasi (gerak melingkar) pada dasarnya mirip dengan gerak translasi (gerak lurus) baik secara teknik analisis atau persamaan-persamaan matematisnya. Pada dasarnya gerak rotasi merupakan gerak lurus yang ditarik ke suatu titik secara terus menerus sehingga lintasannya menjadi melingkar. Gaya yang menarik tersebut disebut dengan gaya sentripetal. Sebelum mempelajari lebih lanjut tentang dinamika rotasi, penting untuk mengetahui hubungan antara besaran-besaran dalam gerak translasi dengan besaran-besaran dalam gerak rotasi. Hal ini dikarenakan keduanya saling berkaitan seperti yang terlihat pada tabel di bawah ini Dinamika Rotasi Dinamik