Jurus jitu : Rahasia konsep perbandingan dalam menyelesaikan soal fisika
Jurus jitu : Rahasia konsep perbandingan dalam menyelesaikan soal FISIKA
Seperti yang sudah pernah saya bahas pada artikel tutorial belajar fisika : semakin paham semakin cinta dengan mudah salah satunya dengan melihat bahwa ilmu matematika adalah ilmu dasar yang dapat diterapkan di semua disiplin ilmu. Hal ini penting saya kemukakan karena banyak siswa yang kesulitan dalam menerapkan perhitungan dalam menyelesaikan soal fisika, sehingga fisika menjadi terasa rumit dan sulit. Padahal dengan memahami konsep matematika dasar dan diterapkan dalam mengerjakan soal fisika, maka soal akan terasa lebih mudah. Salah satu konsep matematika yang sering digunakan dalam mengerjakan soal adalah konsep perbandingan. Dimana dengan kita memahami konsep perbandingan ini maka kita akan lebih mudah menyelesaikan soal, dan konsep ini berlaku untuk semua jenis ilmu. Mari simak penjelasan saya berikut ini
Dasar matematis
Konsep perbandingan merupakan salah satu konsep dasar yang dipelajari di pelajaran matematika, sesuai dengan namanya “perbandingan” yakni membandingkan dua variabel (besaran) atau lebih pada keadaan awal dan akhir. Dalam ilmu matematika untuk tingkat SMP sering kita melihat soal seperti ini- sebuah bangunan yang panjangnya 21 m dibuat model dengan panjang 42 cm. bila tinggi bangunan pada model 15 cm, tentukan tinggi bangunan sebenarnya!
- suatu perkerjakan dapat diselesaikan dalam waktu 50 hari oleh 14 pekerja. Karena suatu hal, setelah bekerja selama 10 hari, perkerjaan terhenti selama 12 hari. Agar pekerjaan dapat diselesaikan tepat pada waktunya maka diperlukan tambahan pekerja sebanyak ... orang
Perhatikan pada soal nomor 1)
Besaran yang dibandingkan antara tinggi bangunan pada model dengan tinggi bangunan sebenarnya. Logikanya jika tinggi bangunan model semakin besar maka tinggi sebenarnya dari bangunan itu juga semakin besar (atau bangunan semakin tinggi) perbandingan dengan sifat seperti ini disebut dengan perbandingan “senilai” atau “berbanding lurus”. Dua besaran dikatakan berbanding lurus jika salah satu besaran diperbesar nilainya maka besaran lainnya juga semakin besar nilainya. Penyelesaian dari soal tersebut adalah
21 m → 42 cm
X → 15 cm
Perhatikan soal nomor 2)
Besaran yang dibandingkan antara jumlah pekerja dengan waktu pengerjaan. Logikanya jika waktu pengerjaannya semakin kecil atau mepet (karena tertunda) maka dibutuhkan jumlah pekerja yang semakin banyak atau besar agar selesai tepat waktu, perbandingan dengan sifat seperti ini disebut dengan perbandingan “berbanding terbalik”. Dua besaran dikatakan berbanding terbalik jika salah satu besaran diperkecil nilainya maka besaran lainnya justru akan semakin besar nilainya. Penyelesaian dari soal di atas adalah
50 hari → 14 orang
Setelah bekerja 10 hari, proses pembangunan terhenti 12 hari maka sisa harinya semakin mepet atau sedikit menjadi
50 – 10 – 12 = 28 hari
40 hari → 14 orang (awalnya)
28 hari → X orang (diinginkan)
Jadi agar sesuai dengan jadwal maka perlu ditambahkan 6 orang.
Besaran yang dibandingkan antara jumlah pekerja dengan waktu pengerjaan. Logikanya jika waktu pengerjaannya semakin kecil atau mepet (karena tertunda) maka dibutuhkan jumlah pekerja yang semakin banyak atau besar agar selesai tepat waktu, perbandingan dengan sifat seperti ini disebut dengan perbandingan “berbanding terbalik”. Dua besaran dikatakan berbanding terbalik jika salah satu besaran diperkecil nilainya maka besaran lainnya justru akan semakin besar nilainya. Penyelesaian dari soal di atas adalah
50 hari → 14 orang
Setelah bekerja 10 hari, proses pembangunan terhenti 12 hari maka sisa harinya semakin mepet atau sedikit menjadi
50 – 10 – 12 = 28 hari
40 hari → 14 orang (awalnya)
28 hari → X orang (diinginkan)
Jadi agar sesuai dengan jadwal maka perlu ditambahkan 6 orang.
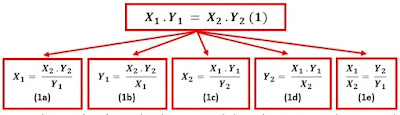
Berdasarkan pembahasan di atas, kini kita dapat mengetahui ada dua jenis tipe perbandingan yakni senilai atau berbanding lurus dan berbanding terbalik. Selain dari logika di atas, kita juga dapat melihat jenis perbandingan antara dua variabel dengan melihat persamaan atau rumusnya. Misalkan sebuah persamaan dituliskan seperti berikut
Indeks “1” (X1 dan Y1) menunjukkan kondisi awal dan Indeks “2” (X2 dan Y2) menunjukkan kondisi akhir. Berdasarkan persamaan di atas, kita dapat mengetahui perbandingan masing-masing variabelnya
Indeks “1” (X1 dan Y1) menunjukkan kondisi awal dan Indeks “2” (X2 dan Y2) menunjukkan kondisi akhir. Berdasarkan persamaan di atas, kita dapat mengetahui perbandingan masing-masing variabelnya
X1 | Y1 | X2 | Y2 | |
X1 | Berbanding Terbalik | Berbanding lurus | Berbanding lurus | |
Y | Berbanding Terbalik | Berbanding lurus | Berbanding lurus | |
X2 | Berbanding lurus | Berbanding lurus | Berbanding Terbalik | |
Y2 | Berbanding lurus | Berbanding lurus | Berbanding Terbalik |
Tips :
1) Agar lebih memahami sifat perbandingan pada tabel di atas, perhatikan letak atau posisi besaran pada persamaan. Jika besaran yang dibandingkan terletak pada satu ruas di kiri atau kanan tanda sama dengan (X1 dan Y1, X2 dan Y2) maka jenis perbandingannya adalah berbanding terbalik, akan tetapi jika besaran yang dibandingkan dipisahkan tanda sama dengan ( X1 dengan X2 dan Y2, X2 dengan X1 dan Y1) maka jenis perbandingannya adalah berbanding lurus.
2) Selain itu jangan terkecoh dengan bentuk persamaannya. Sifat perbandingannya tidak berubah meskipun bentuk persamaannya berubah (dilakukan perkalian silang). Persamaan di atas dapat berubah ditulis juga menjadi
1) Agar lebih memahami sifat perbandingan pada tabel di atas, perhatikan letak atau posisi besaran pada persamaan. Jika besaran yang dibandingkan terletak pada satu ruas di kiri atau kanan tanda sama dengan (X1 dan Y1, X2 dan Y2) maka jenis perbandingannya adalah berbanding terbalik, akan tetapi jika besaran yang dibandingkan dipisahkan tanda sama dengan ( X1 dengan X2 dan Y2, X2 dengan X1 dan Y1) maka jenis perbandingannya adalah berbanding lurus.
2) Selain itu jangan terkecoh dengan bentuk persamaannya. Sifat perbandingannya tidak berubah meskipun bentuk persamaannya berubah (dilakukan perkalian silang). Persamaan di atas dapat berubah ditulis juga menjadi
Dengan memahami sifat-sifat perbandingan ini, kalian dapat menerapkannya pada persamaan atau rumus di semua mata pelajaran asalkan pada persamaan tersebut tidak ada operasional matematis “+” dan atau “-“. Kali ini saya akan menjelaskan penerapan konsep perbandingan tersebut pada mata pelajaran fisika, untuk mata pelajaran lain pada dasarnya sama hanya tinggal menyesuaikan rumus dan besarannya.
Aplikasi pada bidang fisika
Konsep perbandingan sangat bermanfaat jika diterapkan di mata pelajaran fisika karena di mata pelajaran fisika juga banyak dijumpai rumus-rumus. Seperti yang dijelaskan di atas, bahwa konsep perbandingan ini dapat digunakan untuk semua rumus selama tidak ada operasional matematis (+) dan atau (-) jadi dapat digunakan untuk materi fisika tingkat SMP atau SMA.Terdapat beberapa penyesuaian dalam penerapan konsep perbandingan pada mata pelajaran fisika sebelum menggunakan konsep perbandingan ini.
Penyesuaian
Beberapa penyesuaian yang perlu diperhatikan antara lain:
- Pahami soal tipe perbandingan Soal-soal tipe perbandingan biasanya dalam satu besaran mengalami perubahan dikarenakan pengaruh besaran lain yang berubah sehingga antar besaran yang berubah membuat suatu rasio (perbandingan tertentu). Contoh soal tipe perbandingan antara lain
- Perhatikan rumus fisika yang digunakan Karena rumus fisika begitu banyak dengan bentuk yang berbeda-beda maka kita harus dengan cermat dalam menentukan besaran-besaran yang diketahui, yang ditanyakan, dan di bandingkan serta makna dari simbol-simbol dalam rumus tersebut. simbol-simbol itu nantinya akan mengikuti persamaan perbandingan seperti di atas. Beberapa bentuk rumus dalam bidang fisika antara lain
- Perhatikan hubungan antara besaran yang dibandingkan Melanjutkan dari point pertama, karena bentuk rumus di bidang fisika maka hati-hati dalam menentukan hubungan perbandingan antara dua besaran yang dibandingkan, untuk itu pahami dengan benar tips di atas. Berikut contohnya Pada persamaan energi kinetik (Ek = ½ mv2) maka Energi kinetik (Ek) berbanding lurus dengan massa (m) dan kuadrat kecepatan(v2)
- Pahami kondisi awal dan akhir besaran pada soal Dalam soal fisika, kondisi awal dan kondisi akhir suatu besaran bergantung pada kejadian atau peristiwa yang terdapat di soal, untuk itu kalian harus memahami makna dari soal tersebut. soal fisika selain memiliki makna matematis juga memiliki makna fisis yang mana pada dasarnya sebagian besar dapat disimulasikan. Contohnya sebagai berikut
- Perhatikan makna fisis dari rumus fisika yang digunakan Makna fisis yang dimaksudkan disini adalah lebih pada makna persamaan jika ditinjau dari fenomenanya tidak sekedar ditinjau dari sisi matematisnya. Misal hubungan antara massa dan kecepatan dalam rumus energi kinetik di atas,
“sebuah benda yang bermassa 5 kg di dorong dengan gaya F sehingga mengalami percepatan sebesar 2 m/s2. Jika kemudian di atas benda tersebut diletakkan benda lain yang bermassa 3 kg dan didorong dengan gaya yang sama, tentukan besar percepatannya sekarang!”
Pada soal di atas terlihat karena massa yang digunakan berubah (setelah di letakkan benda lain) maka percepatan dari gabungan benda tersebut berubah. Jadi besaran percepatan mengalami perubahan ketika besaran massanya berubah.
Massa (m) berbanding terbalik dengan kuadrat kecepatan (v2)
“sebuah benda bermassa 2,5 kg bergerak dengan kecepatan 20 m/s, selang beberapa lama kemudian benda lain yang bermassa 1,5 kg di letakkan di atas benda pertama. Agar energi kinetiknya tidak mengalami perubahan, maka kecepatan kedua benda adalah?”
Pada soal di atas, dapat kita ketahui
kondisi awal benda
massa 2,5 kg → m1 = 2,5 kg
kecepatan 20 m/s → v1 = 20 m/s
kondisi akhir benda
massa 2,5 + 1,5 = 4 kg → m2 = 4 kg
kecepatan ... m/s → v2 = ... ?
Secara matematis massa berbanding terbalik dengan kuadrat kecepatan, semakin besar massa benda maka kuadrat kecepatannya semakin kecil begitu pula sebaliknya, sedangkan jika ditinjau secara fisis hubungan antara massa dan kecepatan itu memiliki makna semakin besar massa benda (semakin berat) dengan energi yang sama tentu benda akan bergerak lebih lamban (kecepatan berkurang).
Penerapan konsep perbandingan
Penerapan konsep perbandingan dalam bidang fisika (atau mungkin juga bisa digunakan di bidang yang lain) pada dasarnya tidak jauh berbeda dengan matematika, akan tetapi disini saya akan mencoba menjabarkan cara penggunaannya dengan lebih simpel dan efektif (menurut saya ya,,hehehe) dalam menyelesaikan soal tentang perbandingan.Pertama yang perlu dipahami adalah konsep perbandingan memiliki dua jenis yakni berbanding lurus dan berbanding terbalik, hal ini berimbas pada bentuk persamaan perbandingan yang terbentuk. Misalkan untuk dua besaran X dan Y yang dibandingkan Secara umum dapat dituliskan sebagai berikut
Berdasarkan persamaan umum di atas, ada dua hal yang perlu diperhatikan yakni
- Besaran yang ditanyakan : untuk mempermudah dalam perhitungan, letakkan di tempat sebelah kiri atas
- Susunan indeks : ada sedikit perbedaan untuk besaran – besaran yang berbanding lurus dan berbanding terbalik
Rumus hukum II Newton
F = m . a
Persamaan perbandingan antara massa (m) dan percepatan (a) dengan gaya yang digunakan sama (massa berbanding terbalik dengan percepatan)Sebenarnya persamaan di atas dapat dibuktikan secara matematis sebagai berikut
Untuk lebih mudah menghafalnya cukup pahami posisi indeksnya saja, jika besarannya berbanding lurus maka posisi indeks tidak berubah, akan tetapi jika besarannya berbanding terbalik maka posisi indeksnya dibalik juga.
Rumus Energi kinetik
Persamaan perbandingan antara kecepatan (v) dengan energi kinetik (Ek) dengan massa benda yang sama (energi kinetik berbanding lurus dengan kuadrat kecepatan)
Rumus Energi kinetik
Persamaan perbandingan antara kecepatan (v) dengan energi kinetik (Ek) dengan massa benda yang sama (energi kinetik berbanding lurus dengan kuadrat kecepatan)
Perhatikan : jika pada rumus terdapat besaran yang berpangkat, maka dalam persamaan perbandingan pangkatnya juga diikutsertakan.
Rumus hukum Coulomb
Persamaan perbandingan antara gaya coulomb (F), besar muatan (q1 dan q2) serta jarak (r) dengan k adalah konstanta (gaya coulomb sebanding dengan besar muatan dan berbanding terbalik dengan kuadrat jarak
Perhatikan : jika lebih dari satu besaran yang dibandingkan, tetap tuliskan semua besaran tersebut dengan memperhatikan sifat perbandingannya (berbanding lurus atau berbanding terbalik)
Rumus interferensi celah ganda untuk pita terang
Persamaan perbandingan antara jarak dua celah (d), jarak terang ke-n dari terang pusat (P), serta panjang gelombang (λ) dengan jarak celah ke layar dan orde pita terang yang sama (jarak dua celah berbanding terbalik dengan jarak terang ke-n dari terang pusat dan berbanding lurus dengan panjang gelombang)
Perhatikan : jika ada besaran yang tidak berubah (konstan) dalam rumus maka tidak usah diikutkan ke dalam persamaan perbandingan.
Penerapan dalam soal
Soal nomor 1Sebuah mobil bergerak dari titik A ke titik B dan ke titik C seperti gambar
Jika kecepatan mobil dari titik A ke titik B 20 m/s dan kecepatan dari titik B ke titik C 40 m/s maka perbandingan energi kinetik yang dimiliki mobil sewaktu bergerak antara titik A ke B dengan antara titik B ke C adalah ....
a. 1 : 4
b. 1 : 2
c. 2 : 1
d. 4 : 1
b. 1 : 2
c. 2 : 1
d. 4 : 1
pembahasan soal nomor 1:
Soal nomor 2
Dua buah muatan listrik positif Q1 dan Q2 terpisah sejauh r dan saling tolak menolak dengan gaya 120 N. jika muatan Q1 diperbesar 4 kali semula dan jaraknya menjadi 2 kali semula, maka besar gaya tolaknya sekarang adalah ....
a. 30 N
b. 60 N
c. 120 N
d. 240 N
Soal nomor 3
Dua buah peluru A dan B ditembakkan dari senapan yang sama dengan kecepatan awal sama tetapi sudut elevasi benda masing-masing 450 dan 600, maka perbandingan jarak jatuh A dan B adalah ....
Soal nomor 4
Percepatan gravitasi di permukaan planet X adalah 12 kali percepatan gravitasi di permukaan bumi. Jika jari-jari planet X adalah ½ kali jari-jari Bumi. Maka massa planet X adalah ....
a. 2 kali massa Bumi
b. 3 kali massa Bumi
c. 4 kali massa Bumi
d. 6 kali massa Bumi
e 8 kali massa Bumi
Soal nomor 5a. 30 N
b. 60 N
c. 120 N
d. 240 N
pembahasan soal nomor 2:
Dua buah peluru A dan B ditembakkan dari senapan yang sama dengan kecepatan awal sama tetapi sudut elevasi benda masing-masing 450 dan 600, maka perbandingan jarak jatuh A dan B adalah ....
pembahasan soal nomor 3:
Percepatan gravitasi di permukaan planet X adalah 12 kali percepatan gravitasi di permukaan bumi. Jika jari-jari planet X adalah ½ kali jari-jari Bumi. Maka massa planet X adalah ....
a. 2 kali massa Bumi
b. 3 kali massa Bumi
c. 4 kali massa Bumi
d. 6 kali massa Bumi
e 8 kali massa Bumi
pembahasan soal nomor 4:
Gas Argon berada dalam ruangan tertutup saat suhunya berubah menjadi dua kali semula, maka kecepatan gerak partikel gas argon berubah menjadi ....
a. ½ kali semula
b. 1/√2 kali semula
c. √2 kali semula
d. 2 kali semula
e. 4 kali semula
pembahasan soal nomor 5:
Perhatikan gambar!
Dua kubus yang identik dimasukkan dalam dua zat cair (B dan C) yang massa jenisnya berbeda. Bagian kubus yang masuk ke dalam zat cair B 50% dan zat cair C 30%. Perbandingan massa jenis zat B dan C adalah ....
A. 3 : 5
B. 4 : 5
C. 5 : 4
D. 5 : 3
E. 5 : 2
B. 4 : 5
C. 5 : 4
D. 5 : 3
E. 5 : 2
pembahasan soal nomor 6:
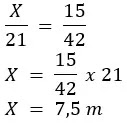


























Comments
Post a Comment